3일동안 딜런 강사님의 기초적인 통계를 리뷰하는 시간을 가졌다.
학과 과목에서 들었던 discrete math 및 linear algebra가 실질적으로 도움이 많이 되었고 막상 학과에선 이 과목들이 왜
필수과목일까 (discrete은 필수, linear는 선택이었음) 생각했고, 안 그래도 수학이 많이 약하다고 생각했기 때문에 엄청나게 노력해서 pass했던 기억이 있었는데 이번 리뷰를 통해서 다시 한번 maching learning을 할려면 이 정도는 기본으로 알고 있어야겠구나를 느꼈고 이번 학습일지는 1,2일치 내주셨던 문제를 토대로 내가 풀었던 방식을 작성하면서 3일 과정을 요약해보고자 한다.
Latex를 사용해서 해보려 했으나(학과과정에선 latex를 썼다) 생각보다 티스토리에서 작성하는 게 오래 걸려서 일단 손으로 풀었던 내용을 작성한다.
<Set, Function >

풀이:


풀이:


풀이:

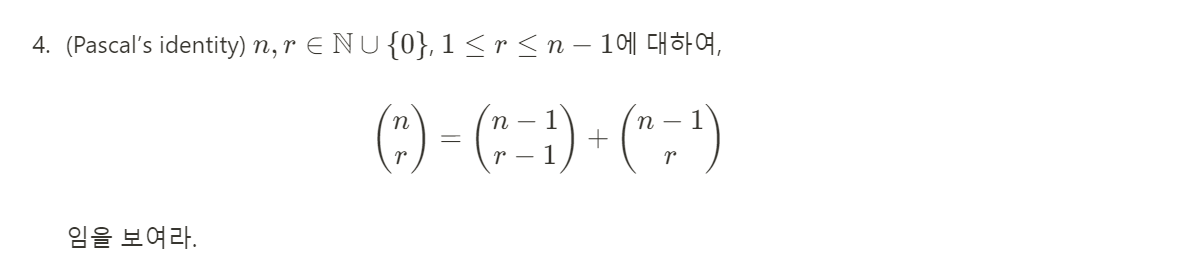
풀이:

<Probability and Distributions>

풀이 :
- 첨예도 : 데이터 분표의 꼬리 부분이 얼마나 두꺼운지 측정하는 통계적 지표 (Kurtosis)
- 정규분포의 첨예도를 기준 - 양(값이 3보다 큼: 중앙에 데이터가 몰려있음) / 음(3보다 작음, 분포의 꼬리가 얇고 분산되어있음) / 정규 ( 정규분포)
- 데이터의 분포가 얼마나 뾰족하거나 평평한지를 통해 데이터 내에 극단적인 값이 있는지 판단
- 왜도: 데이터 분포의 비대칭성을 측정하는 통계적 지표(skewness)
- 데이터가 평균값을 중심으로 좌우로 얼마나 분포되어 있는지 확인
- Right skewed(or Positively skewed): 평균이 중앙값보다 큼(극단적으로 큰값이 존재) (꼬리가 오른쪽으로)
- Left-skewed(or Negatively skewed) : 평균이 중앙값보다 작음(극단적으로 큰값이 존재할 가능성 낮음) (꼬리가 왼쪽으로)
- 데이터의 중심경향성 분석 및 아웃라이어 검출 유용함
Python Implementation
import numpy as np
import scipy.stats as stats
import matplotlib.pyplot as plt
# 데이터 생성 (예시: 정규분포, 양의 왜도 분포, 음의 왜도 분포)
data_normal = np.random.normal(0, 1, 1000)
data_pos_skew = np.random.exponential(1, 1000)
data_neg_skew = np.random.lognormal(0, 1, 1000) - 3
# kurtosis/skewness 계산
kurtosis_normal = stats.kurtosis(data_normal)
skewness_normal = stats.skew(data_normal)
kurtosis_pos_skew = stats.kurtosis(data_pos_skew)
skewness_pos_skew = stats.skew(data_pos_skew)
kurtosis_neg_skew = stats.kurtosis(data_neg_skew)
skewness_neg_skew = stats.skew(data_neg_skew)
# 결과
print(f"Normal Distribution: Kurtosis = {kurtosis_normal}, Skewness = {skewness_normal}")
print(f"Positive Skew Distribution: Kurtosis = {kurtosis_pos_skew}, Skewness = {skewness_pos_skew}")
print(f"Negative Skew Distribution: Kurtosis = {kurtosis_neg_skew}, Skewness = {skewness_neg_skew}")
#시각화
plt.figure(figsize=(12, 6))
plt.subplot(1, 3, 1)
plt.hist(data_normal, bins=30, alpha=0.7, color='blue')
plt.title('Normal Distribution')
plt.subplot(1, 3, 2)
plt.hist(data_pos_skew, bins=30, alpha=0.7, color='green')
plt.title('Positive Skew Distribution')
plt.subplot(1, 3, 3)
plt.hist(data_neg_skew, bins=30, alpha=0.7, color='red')
plt.title('Negative Skew Distribution')
plt.tight_layout()
plt.show()
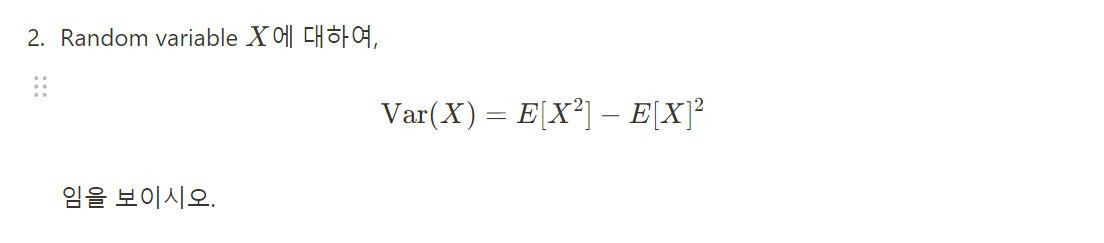
풀이:
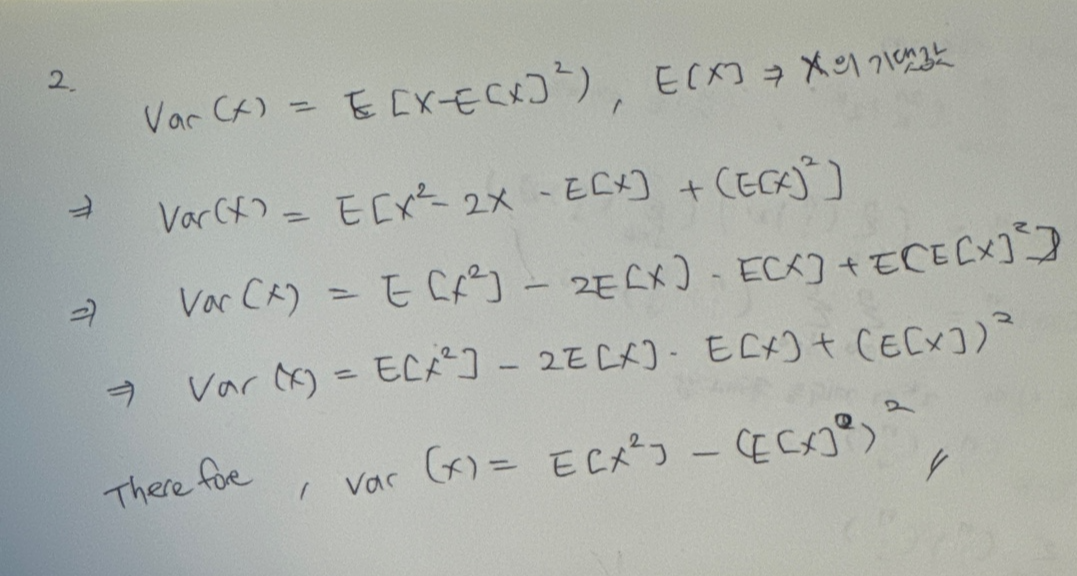
<추가 개념 리뷰>
- Conditional Probability : 조건부 확률 -> 특정 사건이 일어났다는 조건 아래 다른 사건이 일어날 확률
P(B∣A)=P(A) / P(A∩B) : 사건 A가 발생했을 때, 다른 사건 B가 발생할 확률 : P(B|A) - Uniform Distribution, Bionmial Distribution, Normal Distribution, Poisson Distribution
Uniform Distribution Python Code:
import numpy as np
import matplotlib.pyplot as plt
# 연속형 균등 분포에서 난수 생성 (0과 1 사이)
data = np.random.uniform(0, 1, 1000)
# 히스토그램 시각화
plt.hist(data, bins=30, density=True, alpha=0.6, color='g')
plt.title('Uniform Distribution [0, 1]')
plt.xlabel('Value')
plt.ylabel('Frequency')
plt.show()
Binomial Distribution Python Code:
import scipy.stats as stats
# 파라미터
n = 20 # 시행 횟수
p = 0.5 # 성공 확률
k = 3 # 성공 횟수
# binomial에서 k번 성공할 확률
prob = stats.binom.pmf(k, n, p)
print(f"P(X = {k}) = {prob:.4f}")
Normal Distribution Python Code:
import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as stats
# 평균 / 표준 편차
mu = 0
sigma = 1
# 정규 분포를 따르는 데이터 생성
data = np.random.normal(mu, sigma, 1000)
# histogram
plt.hist(data, bins=30, density=True, alpha=0.6, color='g')
# value,frequency
xmin, xmax = plt.xlim()
x = np.linspace(xmin, xmax, 100)
p = stats.norm.pdf(x, mu, sigma)
plt.plot(x, p, 'k', linewidth=2)
plt.title('Normal Distribution with mean=0 and std=1')
plt.xlabel('Value')
plt.ylabel('Frequency')
plt.show()
Poisson Distribution Python Code:
import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as stats
# 파라미터
lambda_val = 4 # 평균 사건 발생 횟수 (lambda)
k = 5 # 사건 발생 횟수
# k번 등장할 확률
prob = stats.poisson.pmf(k, lambda_val)
print(f"P(X = {k}) = {prob:.4f}")
# random, poisson
data = np.random.poisson(lambda_val, 1000)
# histogram
plt.hist(data, bins=30, density=True, alpha=0.6, color='g')
# pmf
x = np.arange(0, 15)
pmf = stats.poisson.pmf(x, lambda_val)
plt.plot(x, pmf, 'k', linewidth=2)
plt.title(f'Poisson Distribution (lambda = {lambda_val})')
plt.xlabel('Number of events')
plt.ylabel('Probability')
plt.show()< Hypothesis Test 개념 리뷰>
1. Statistical Inference (통계적 추론)
- 통계적 추론: 표본의 통계량으로부터 모집단의 모수를 추정하는 과정.
- 점추정 (Point Estimation): 표본의 통계치 하나로 모수를 추정하는 방법.
- 구간추정 (Interval Estimation): 점추정한 값을 기준으로 신뢰구간을 부여하여 모수를 추정하는 방법.
1.1 Point Estimation (점추정)
- 단일 표본을 통해 특정 값을 추정.
- 대표성 있는 표본이 필요하지만, 단일 값으로 전체 모집단을 대표하기에는 한계가 있음.
1.2 Interval Estimation (구간추정)
- 구간추정: 모평균의 구간을 추정하여, 신뢰구간을 설정.
- 신뢰수준 (Confidence Level): 특정 구간이 참 모수를 포함할 확률.
- 신뢰구간 (Confidence Interval): 모수가 해당 구간 내에 있을 가능성을 나타냄.
- 신뢰구간의 의미는 표본의 신뢰구간이 모집단의 모수를 포함할 확률로 이해해야 함.
2. Hypothesis Test (가설검정)
- 가설검정: 모집단의 특성에 대한 가설을 설정하고 표본을 통해 가설을 검정하는 과정.
- 귀무가설 (Null Hypothesis, H0H_0): 기본 가정으로 채택하고자 하는 가설.
- 대립가설 (Alternative Hypothesis, H1H_1): 대체 가설로, 귀무가설이 기각될 경우 채택되는 가설.
2.1 Test Statistic (검정통계량)
- 표본을 통해 얻은 통계량으로 가설을 검정하기 위한 기준.
2.2 Type 1 & Type 2 Errors (제 1종 및 제 2종 오류)
- 제 1종 오류 (Type 1 Error): 실제로 귀무가설이 참일 때, 이를 기각하는 오류.
- 제 2종 오류 (Type 2 Error): 실제로 대립가설이 참일 때, 귀무가설을 채택하는 오류.
2.3 Significance Level & Critical Region (유의수준과 기각역)
- 유의수준 (Significance Level): 제 1종 오류를 범할 최대 허용 확률 (α\alpha).
- 기각역 (Critical Region): 귀무가설을 기각하는 통계량의 영역.
2.4 One-sided vs. Two-sided Test
- One-sided Test: 대립가설이 한 방향으로만 설정되는 검정.
- Two-sided Test: 대립가설이 양방향으로 설정되는 검정.
2.5 p-value
- p-value: 귀무가설이 참일 때, 현재 데이터를 관찰할 확률.
- 작은 p-value는 귀무가설이 참일 가능성이 낮음을 시사.
솔직히 3일동안의 과정은 내가 어느정도 학과에서 배웠고 (솔직히 지금은 많이 잊어먹어서 다시 따라 가는게 급급했지만 ) 증명하는데 있어서 어려움을 예전에 discrete math를 하면서 초반에 많이 겪었기 때문에 만약 비전공자였다면 매우 힘들었을 시간이었다. 강사님이 말한 이 과정은 절대 3일만에 해결되는 부분이 아니기 때문이다. 아무래도 난 수학에 큰 강점이 있는 사람은 아니지만 많은 오류와 (지금은 gpt와 여러 좋은 사이트들이 많이 생겨서 좋아졌지만) 모르는 증명식이 나왔을 때 벙찌는 그런 감정이 들어야 (시험을 보면서) 진짜 제대로 배우는 것 같다. (이 과정이 시간이 엄청 걸린다) 하지만 전체적인 개념면에선 다시 한번 짚을 수 있어서 좋았고 증명이나 여러 theorem, 물론 hypothesis test나 distribution 같은 경우 머신러닝에는 필수겠지만, 수학적으로 증명할 때 솔직히 재미는 없었다고 생각한다. 강사님이 말한 "수학 문제를 오랫동안 끈질지게 붙잡고 늘어지는 사람"이 대체적으로 끈기력이나 성과를 거둘 확률이 높다라고 말한 것은 어느정도 동의하지만, 이 과정 이상으로 깊숙히 파고들고 싶단 생각은 들지 않는다.
'AI' 카테고리의 다른 글
| <7일차> ML 경진대회 : Regression Wrap up (5) | 2024.09.20 |
|---|---|
| <6일차> LLM Project : 스포츠 규정에 관하여 답하는 QA Engine 개발 (3) | 2024.08.27 |
| <4일차> Git (0) | 2024.08.09 |
| <3일차> 프로젝트 수행을 위한 이론 : python + langchain(및 LLM + RAG (0) | 2024.08.06 |
| <2일차> 컴퓨터 공학 개론 Review (0) | 2024.07.25 |